Tutorial KmPlot

KmPlot adalah tool untuk memplot (membuat grafik) berdasarkan suatu fungsi/persamaan matematika. Dengan tool ini, akan lebih cepat membuat kurva dari fungsi matematika daripada kita menggunakan GNU Octave ataupun GeoGebra. Untuk perhitungan yang lebih kompleks, analisa dengan Octave atau python tetap diperlukan. Tool ini sangat powerful untuk demo di kelas atau ketika kita menginginkan plot kasar dari suatu persamaan matematik, bisa karena belum tahu atau lupa.

Instalasi

Untuk menginstall KmPlot pada Ubuntu cukup mudah, yakni dengan perintah berikut:

sudo apt install kmplot

Untuk mengeceknya, buka dash (tekan Super) dan ketik Km, maka Kmplot akan muncul pada layar Dash. Klik ikon tersebut dan akan tampilan seperti dibawah.

Tampilan awal KmPlot

Tampilan diatas adalah tampilan defautl KmPlot. Untuk memplot sebuah fungsi, klik menu "Create", maka akan muncul 5 menu baru. Jika anda masih awam dengan tipe-tipe plot tsb, penjelasan sederhanya adalah sbb.

1. Cartesian Plot
Pada mode Cartesian Plot, fungsi yang diplot adalah fungsi eksplisit. Fungsi eksplisit artinya f(x) dan x ditulis dalam yang terpisah, f(x) disebelah kiri dan x di sebelah kanan. Contoh fungsi ini adalah, $f(x)=x^2$, $f(x)=x^2+x-6$, dsb.
2. Parametric Plot
Pada fungsi parametrik, $x$ dan $y$ tidak terhubung secara langsung, biasanya dihubungkan oleh variabel $t$. Contoh fungsi parametrik adalah $f_x(t)=10+t, f_x(t)=sin(t)$, dll.
3. Polar Plot
Polar plot adalah plot fungsi pada bidang plot/lingkaran. Fungsi yang diplot pada polar plot biasanya merupakan fungsi yang bergantung pada variabel radius (r) dan sudut ($\theta$). Contoh fungsi yang bisa diplot pada polar plot misalnya pola keterarahan sumber suara, $I=\dfrac{I_0}{r^2}$
4. Implicit Plot
Implicit plot adalah kebalikan dari eksplisit plot, yakni variabel x dan y ditulis pada ruas yang sama. Contohnya $x^2+y^2=24$
5. Differential Plot
Differential plot adalah plot turunan dari fungsi, bisa turunan pertama, turunan kedua atau ke $n$. Contoh, $f'(x)=2x$.

Contoh

Contoh-contoh dibawah adalah beberapa fungsi yang saya plot dengan KmPlot. Fungsi-fungsi tsb juga merupakan soal ETS Matematika 1 tahun 2016 pada Departement Teknik Fisika ITS.
1. Grafik $x^2-3x+2$ (Cartesian Plot)

2. Grafik y= x² + 4 (Cartesian Plot)
Grafik ini adalah grafik y= x² yang digeser keatas sejauh 4 titik.

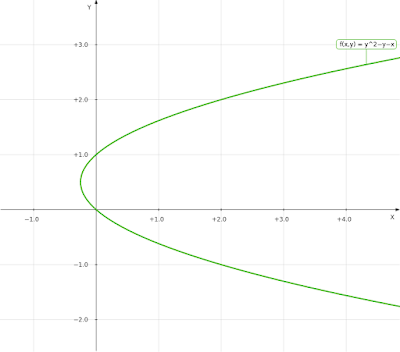
3. Grafik x= y² - y
Grafik ini ditulis dalam Implicit Plot sebagai: $y^2-y-x$  

4. Grafik persamaan garis 4x+9y=36  Grafik diatas adalah persamaan garis lurus yang diplot melalui Implicit plot dimana memotong sumbu x pada x=9 dan memotong sumbu y pada y=4.

Menggunakan Slider: Contoh pada gerak parabola

Gerak parabola merupakan konsep gerak diperlambat pada Fisika. Misalkan sebuah benda bergerak sebagai berikut (penulisan sesuai KmPlot >> Parametric Plot):

1. v_0=20 (Masukkan pada edit >> constant)
2. f_x(t, α) = v_0∙cos(α)∙t (Untuk memasukkan alfa, klik tanda gear)
3. f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2 
4. Centang pada Slider >> slider No.1 

Untuk memunculkan slider,  klik View >> show slider. Ubah nilai max pada slider 1 menjadi 100, dan gerakkan slider dari 0 ke 100, saya sarankan menggunakan keyboard panah kanan daripada menggunakan mouse. Jangan lupa merubah setting sudut (angle) dari radian ke degree pada Setting >> Configure KmPlot. Maka trajectory gerak parabola akan terlihat dengan mengubah nilai pada slider tsb dimana nilai tsb adalah nilai sudut α. Sebagai bukti, jarak maksimum gerak parabola dirumuskan sbb:
$$x_{max} = \dfrac{V_0^2*\sin{(2\alpha)}}{g}$$
Sehingga jika menempatkan slider pada 76 diperoleh jarak pada tinggi maksimum 18.79 seperti tampak pada grafik dibawah.

Selamat mencoba!